In previous notes, we have talked about how adding additional viewpoints of a scene can greatly enhance our knowledge of the said scene. We focused on
the epipolar geometry setup in order to relate points of one image plane to points in the other without extracting any information about the 3D scene. In these lecture notes, we will discuss how to recover information about the 3D scene from multiple 2D images.
I will talk about 4 parts:
- Triangulation: the process of determining the location of a 3D point given its projections into two or more images.
- Affine structure from motion
- Perspective structure from motion
Triangulation
We have two cameras with known camera intrinsic parameters $K$ and $K'$ respectively. We also know the relative orientations and offsets $R,T$ of the cameras with respect to each other. We can also get precise locations of $p$ and $p'$ in the image.
A $\textbf{Naive}$ way to find the point $P$ in 3D is to find the intersection of sight lines $l$ and $l'$ which are defined by the camera centers $O_1,O_2$ and image locations $p,p'$.
An image explains this: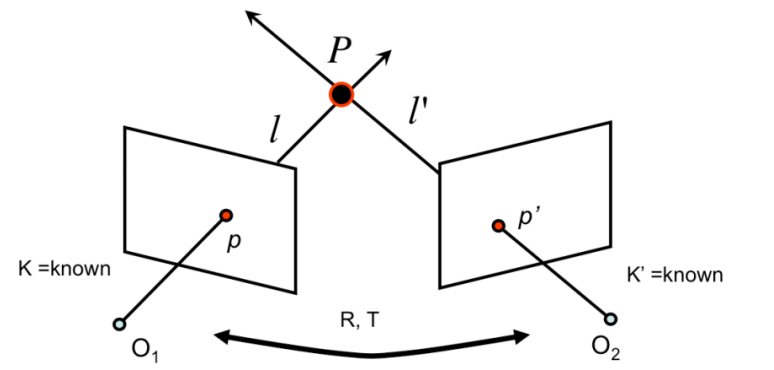
Although this process is both strightforward and mathematically sound, it doesn't work well because of the noisy observations $p$ and $p'$ and noise camera calibration parameter. Next I will show linear and unlinear method to solve this.
A linear method for triangulation
Let $p=MP=(x,y,1)$ and $p'=M'P(x',y',1)$. Notice that $p\times (MP)=0$. Thus we immediately derive three constraints:
where $M_i$ is the $i$-th row of the matrix $M$. Using the constraints from both images, we can formulate a linear equation of the form $AP=0$ where
The equation can be solved using our best friend $\textbf{SVD}$ to find a best linear estimation of $P$. This method can easily handles multi views by just appending additional rows to $A$.
However, this method is not suitable for projective reconstruction. Since if we apply a projective transformation $H$ to the scene, $M,M'$ become $MH^{-1},M'H^{-1}$. Therefore, we will solve $(AH^{-1})(HP)=0$. Since $\textbf{SVD}$ solves for the constraint that $||P||=1$ which is not invariant under a projective transformation $H$. So this method often can't find the optimal solution to triangulation problem.
Code implementation
'''
LINEAR_ESTIMATE_3D_POINT given a corresponding points in different images,
compute the 3D point is the best linear estimate
Arguments:
image_points - the measured points in each of the M images (Mx2 matrix)
camera_matrices - the camera projective matrices (Mx3x4 tensor)
Returns:
point_3d - the 3D point
'''
def linear_estimate_3d_point(image_points, camera_matrices):
M1 = camera_matrices[:,0,:]
M2 = camera_matrices[:,1,:]
M3 = camera_matrices[:,2,:]
A = np.zeros((2*image_points.shape[0], 4))
A[::2,:] = image_points[:,0:1]*M3 - M1
A[1::2,:] = image_points[:,1:2]*M3 - M2
_,_,Vt = np.linalg.svd(A)
point_3d = Vt[-1,0:3]/Vt[-1,3]
return point_3dA nonlinear method for triangualtion
The nonlinear method is to find the best least-squares estimate of the $\textbf{reprojection error}$ of $\hat{P}$:
If there are more than two images:
If we set $e_i$ to be a $2\times1$ vector $e_i=M_i\hat{P}-p_i$. The method we use here is Gauss-Newton whose key insight is to linearize the residual function $e$ near the current estimate $\hat{P}$:
Subsequently, the minimization problem transforms into
For the triangulation problem with $N$ images, the solution is:
where
and
Iteratively use the $\delta_P$ to update $\hat{P}$ until convergence. However the Gauss-Newton method algorithm gives no guarantee of convergence. So, it is always useful in practice to put an upper bound on the number of updates made to the estimate.
Code implementation
- implement reprojrction error:
''' REPROJECTION_ERROR given a 3D point and its corresponding points in the image planes, compute the reprojection error vector and associated Jacobian Arguments: point_3d - the 3D point corresponding to points in the image image_points - the measured points in each of the M images (Mx2 matrix) camera_matrices - the camera projective matrices (Mx3x4 tensor) Returns: error - the 2Mx1 reprojection error vector ''' def reprojection_error(point_3d, image_points, camera_matrices): error = np.zeros((2*image_points.shape[0],)) # pdb.set_trace() if point_3d.shape[-1] == 3: point_3d = np.hstack((point_3d, 1)) reprojected_points = camera_matrices@point_3d reprojected_points = reprojected_points[:,0:2]/reprojected_points[:,2:3] error[::2] = reprojected_points[:,0] - image_points[:,0] error[1::2] = reprojected_points[:,1] - image_points[:,1] return error - implement jacobian
''' JACOBIAN given a 3D point and its corresponding points in the image planes, compute the reprojection error vector and associated Jacobian Arguments: point_3d - the 3D point corresponding to points in the image camera_matrices - the camera projective matrices (Mx3x4 tensor) Returns: jacobian - the 2Mx3 Jacobian matrix ''' def jacobian(point_3d, camera_matrices): if point_3d.shape[-1] == 3: point_3d = np.hstack((point_3d, 1)) projected_points = camera_matrices@point_3d jacobian_matrix = np.zeros((2*camera_matrices.shape[0], 3)) jacobian_matrix[::2,0] = camera_matrices[:,0,0]/projected_points[:,2] - camera_matrices[:,2,0]*projected_points[:,0]/(projected_points[:,2]**2) jacobian_matrix[1::2,0] = camera_matrices[:,1,0]/projected_points[:,2] - camera_matrices[:,2,0]*projected_points[:,1]/(projected_points[:,2]**2) jacobian_matrix[::2,1] = camera_matrices[:,0,1]/projected_points[:,2] - camera_matrices[:,2,1]*projected_points[:,0]/(projected_points[:,2]**2) jacobian_matrix[1::2,1] = camera_matrices[:,1,1]/projected_points[:,2] - camera_matrices[:,2,1]*projected_points[:,1]/(projected_points[:,2]**2) jacobian_matrix[::2,2] = camera_matrices[:,0,2]/projected_points[:,2] - camera_matrices[:,2,2]*projected_points[:,0]/(projected_points[:,2]**2) jacobian_matrix[1::2,2] = camera_matrices[:,1,2]/projected_points[:,2] - camera_matrices[:,2,2]*projected_points[:,1]/(projected_points[:,2]**2) return jacobian_matrix - nonliear method
''' NONLINEAR_ESTIMATE_3D_POINT given a corresponding points in different images, compute the 3D point that iteratively updates the points Arguments: image_points - the measured points in each of the M images (Mx2 matrix) camera_matrices - the camera projective matrices (Mx3x4 tensor) Returns: point_3d - the 3D point ''' def nonlinear_estimate_3d_point(image_points, camera_matrices): points_3d = linear_estimate_3d_point(image_points, camera_matrices) for i in range(10): e = reprojection_error(points_3d, image_points, camera_matrices) J = jacobian(points_3d, camera_matrices) sigma = np.linalg.pinv(J.T@J)@J.T@e points_3d = points_3d - sigma return points_3dAffine structure from motion
In previous section, we see how we can go beyond two views of a scene to gain information about the 3D scene. This section we will see how can we simultaneously determine both the 3D structure of the scene and the parameter of the camera in what is known as structure from motion(sfm).
Let's formally introduce this problem: suppose we have $m$ cameras with camera transformations $M_{i}$ encoding both extrinsic and intrinsic parameter. We have $n$ 3D points denoted as $X_j$. The location of $X_j$ projected to the image of camera $i$ using projective transformation $M_i$ is represented as $x_{ij}$. The aim of sfm is to recover both the structure of the scene (the $n$ 3D points $X_j$) and the motion of the cameras (the $m$ projection matrices $M_i$) from all observation $x_{ij}$.
Now we will start with a simpler problem: assume the cameras are affine or weak-perspective. Without the perspective scaling operation, it's mathematically easy for deriving this problem.
Let's first look at the property of affine transformation:
Thus we can compactly reprensent any camera matrix in the format $M_{\text{affine}}=[A \quad b]$. So we can use the affine camerae model to express the relationship from a point $X_j$ in 3D and the corresponding observations in each affine camera. Returning to our problem, we need to estimate $m$ matrices $M_i$ and $n$ coordinates $X_j$, for a total of $8m+3n$ unknowns. Each observation creates $2$ constraints, so there are $2mn$ equations in $8m+3n$ unknowns. Once we have enough corresponding points in each image, we can use $\textbf{factorizaion}$ method to solve which will be covered in next section.
The Tomasi and Kanade factorization method
This method consists of two major steps: the data centering step and the actual factorizaion step.
Let's first begin with the data centering step:
Recall that:
So $\hat{x}_{ij}$:
Notice that the centered $x_{ij}$ and $\hat{X}_j$ are only related by $A_i$. So we can formulate it in matrix form:
where $D \in \mathbb{R}^{2m\times n} $, $M \in \mathbb{R}^{2m\times 3}$(comprises the camera matrices $A_1,\dots A_m$) and $S\in \mathbb{R}^{3 \times 2n}$(comprises the 3D points $\hat{X}_1,\dots \hat{X}_n$).
Observe that $\text{rank}(D)=3$. Thus we can use $\textbf{SVD}$ to get a best-3 estimation of $D$:
Notice that $U_3$ is a $2m\times 3$ matrix, which is the same size as motion matrix $M$, so as $\Sigma_3 V_3^T$ to structure matrix $S$. In their paper, they concluded that a robust choice of the factorization is $M=U_3 \sqrt{\Sigma_3}$ and $S=\sqrt{\Sigma_3}V_3^T$
However affine ambiguity exists: $D=(MA)(A^{-1}S)$. So $M$ and $S$ are determined up to a multiplication by a common matrix. When a reconstruction has affine ambiguity, it means that parallelism is preserved, but the metric scale
is unknown.
Code implementation
'''
FACTORIZATION_METHOD The Tomasi and Kanade Factorization Method to determine
the 3D structure of the scene and the motion of the cameras.
Arguments:
points_im1 - N points in the first image that match with points_im2
points_im2 - N points in the second image that match with points_im1
Both points_im1 and points_im2 are from the get_data_from_txt_file() method
Returns:
structure - the structure matrix
motion - the motion matrix
'''
def factorization_method(points_im1, points_im2):
centered_points_im1 = points_im1[:,:2] - np.mean(points_im1[:,:2], axis=0)
centered_points_im2 = points_im2[:,:2] - np.mean(points_im2[:,:2], axis=0)
D = np.concatenate((centered_points_im1,centered_points_im2), axis=1).T
U, S, Vt = np.linalg.svd(D)
U3 = U[:,:3]
S3 = np.diag(S[:3])
V3 = Vt[:3,:]
motion = U3 @ np.sqrt(S3)
structure = np.sqrt(S3) @ V3
center_im1 = np.mean(points_im1[:,:2], axis=0)
center_im2 = np.mean(points_im2[:,:2], axis=0)
b = np.concatenate((center_im1, center_im2))
centered_3d = np.linalg.lstsq(motion, b, rcond=None)[0]
structure = structure + centered_3d.reshape(3,1)
return structure, motionPerspective structure from motion
After studying the simplified affine structure from motion, let's consider the general case for projective cameras $M_i$ which contains 11 degrees of freedom. Similar to the affine case where the solution can be found up to an affine transformation, solutions for structure and motion can be determined up a projective transformation in the general case: we can always arbitrarily apply a 4×4 projective transformation $H$ to the motion matrix, as long as we also transform the structure matrix by the inverse transformation $H^{-1}$. The resulting observations in the image plane will still be the same.
As in the affine case, let's first formulate the problem: we want to estimate $m$ motion matrices $M_i$ and $n$ 3D points $X_j$ from $mn$ observations $x_{ij}$. Because cameras and points can only be recovered up to a $4\times 4$ projective transformations up to scale (15 parameters), we have $11m+3n-15$ unknowns in $2mn$ equations.
The algebraic approach
Since $M_1,M_2$ are up to a projection transformation $H$. So we can consider a $H$ such that the first camera projrction matrix $M_1H^{-1}$ is canonical (i.e. $\tilde{M}_1=M_1H^{-1}=[I\quad 0]$). Thus:
Key observation:
which must remind you the general definition of the Fundamental matrix $p'^TFp=0$. If we set $F=[b]_{\times}A$, then extracting A and b simply breaks down to a decomposition problem.
Observation again, we use the property of cross product:
Since $F$ is singular, we can use $\textbf{SVD}$ to get $b$ with $||b||_2=1$.
Observation again: if we set $A=-[b]_{\times}F$, we can verify that this definition satisfies $F=[b]_{\times}A$:
Thus we get two expressions for camera matrices $M_1H^{-1}$ and $M_2H^{-1}$:
Notice that $F^Tb=0$ and $F^Te'=0$. So we can replace $b$ with epipolar $e'$:
Determining motion from the Essential matrix
TBD(Since this section contains complicated math which I'm not familiar with.)
code implementation
- Get four initial extrinsic matrices.
''' ESTIMATE_INITIAL_RT from the Essential Matrix, we can compute 4 initial guesses of the relative RT between the two cameras Arguments: E - the Essential Matrix between the two cameras Returns: RT: A 4x3x4 tensor in which the 3x4 matrix RT[i,:,:] is one of the four possible transformations ''' def estimate_initial_RT(E): U,D,Vt = np.linalg.svd(E) W = np.array([[0,-1,0],[1,0,0],[0,0,1]]) Q1 = U.dot(W).dot(Vt) Q2 = U.dot(W.T).dot(Vt) R1 = np.linalg.det(Q1)*Q1 R2 = np.linalg.det(Q2)*Q2 t1 = U[:,2] t2 = -U[:,2] RT = np.zeros((4,3,4)) RT[0,:,:3] = R1 RT[0,:,3] = t1 RT[1,:,:3] = R1 RT[1,:,3] = t2 RT[2,:,:3] = R2 RT[2,:,3] = t1 RT[3,:,:3] = R2 RT[3,:,3] = t2 return RT - Filter out the matrix
'''
ESTIMATE_RT_FROM_E from the Essential Matrix, we can compute the relative RT
between the two cameras
Arguments:
E - the Essential Matrix between the two cameras
image_points - N measured points in each of the M images (NxMx2 matrix)
K - the intrinsic camera matrix
Returns:
RT: The 3x4 matrix which gives the rotation and translation between the
two cameras
'''
def estimate_RT_from_E(E, image_points, K):
RT_initall = estimate_initial_RT(E)
M1 = K.dot(np.hstack((np.eye(3), np.zeros((3,1)))))
count = 0
idx = -1
for i in range(4):
M2 = K.dot(RT_initall[i,:,:])
used_image_points = image_points[:,:2,:]
camera_matrices = np.concatenate((M1[np.newaxis,:,:], M2[np.newaxis,:,:]), axis=0)
total = 0
for j in range(used_image_points.shape[0]):
point_3d = nonlinear_estimate_3d_point(used_image_points[j,:,:], camera_matrices)
if point_3d[2] > 0 and ((point_3d-RT_initall[i,:,-1]).dot(RT_initall[i,:,:3]))[-1] > 0:
total+=1
if total > count:
count = total
idx = i
if idx == -1:
print("No valid RT found")
return None
return RT_initall[idx,:,:]Conclude
Let's conclude the whole pipline of sfm. Suppose we have calibrated camera with known $f_x=f_y$ and $c_x=c_y=0$ (i.e. known intrinsic parameter $K$) and we precisely know the locations of each point $p$ on each image:
- Use Normalized Eight-Point Algorithm to compute Fundamental matrix $F$.
- Use the relation between $F$ and $E$: $E=K^T\cdot F\cdot K$ to compute Essential matrix $E$
- We can Determine motion from the Essential matrix $E$. We get 4 $[R\quad T]$ matrices.
- Use the nonliear method to estimate the 3D point under each $[R \quad T]$ matrix to filter out the correct matrix.
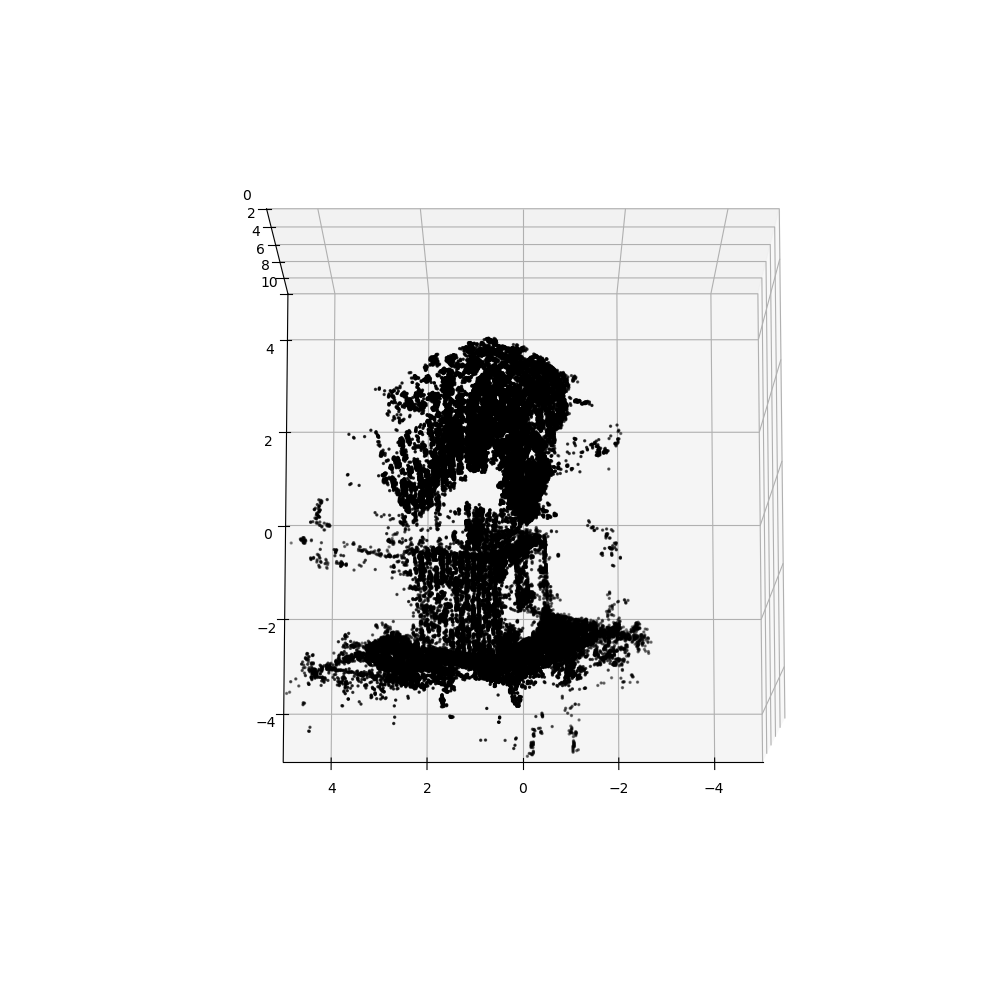
Finally, let me show the final result of corresponding assignment from CS231A: