Traditionally, the main idea of stereo is to use corresponding points $p$ and $p'$ to estimate the location of a 3D point by point $P$ using triangulation. But how do we knwow a point $p$ in one image actually corresponds to $p'$ in another. I will talk about alternative techniques that work well in reconstructing the 3D structure.
Active stereo - mitigating the correspondence problem
The main idea is to replace one of the cameras with a device that interacts with the 3D environment, usually by projecting a pattern onto the object that is easily identifiable from the second camera. The new projector-camera pair defines the same epipolar geometry that we introduced for camera pairs. The image plane of the replaced camera is replaced with a projector virtual plane.
As the figure shows: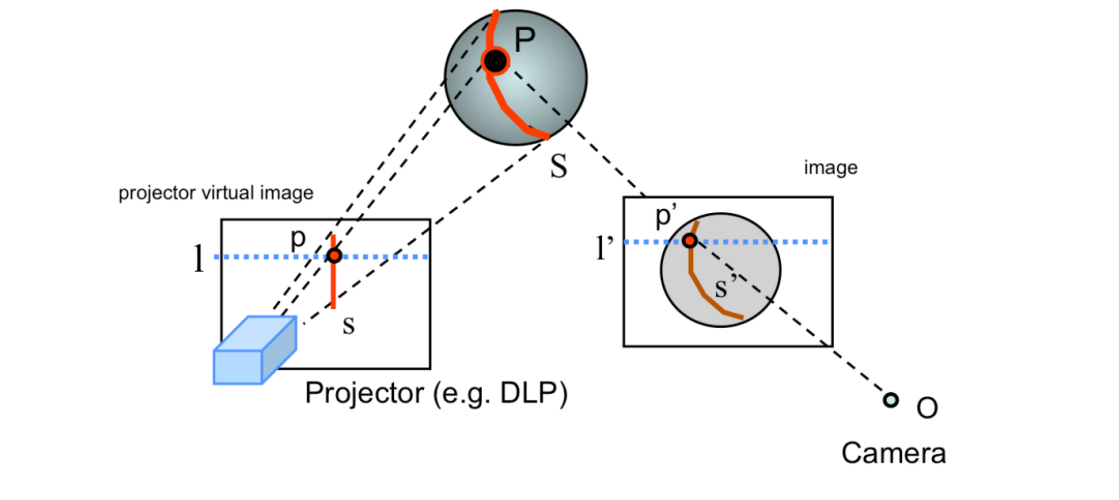
The projector projects a point $p$ in the virtual plane onto the target object, producing a point $P$ in 3D space. This point $P$ can should be observed in the second camera as point $p'$. Since we know the color, intensity... of the projection, so we can easily discover the correspoind observation in the second camera $p'$.
A common strategy in active stereo is to project a vertical stripe $s$ instead of a single point $p$. Like above figure shows, a vertical stripe $s$ in the projector virtual plane is colored red. After observing from the camare, it may become brown and can be easily discovered. If the projector and camera are parallel or rectified, then correspoind points can be easily found by intersectiong $s'$ with the horizontal epipolar lines (I have covered in epipolar geometry section). From correspondences, we can easily reconstruct the all 3D points on the stripe $S$ using triangulation methods I have covered in the last section. If we swip the line $s$ across the scene and repeat the process, we can reconstruct the entire shape of all visible objects in the scene.
The prerequisite of the algorithm to work is that the projector and the camera should be calibrated. We can
first calibrate the camera using a calibration rig. Then, by projecting known stripes onto the calibration rig, and using the corresponding observations in the newly calibrated camera, we can set up constraints for estimating the projector intrinsic and extrinsic parameters.
One limitation of projecting a single stripe onto objects is that it is rather slow, as the projector needs to swipe across the entire object. Furthermore, this means that this method cannot capture deformations in real time. A natural extension is to instead attempt to reconstruct the object from projecting a single frame or image. The idea is to project a known pattern of different stripes to the entire visible of the object, instead of a single stripe. The colors of these stripes are designed in such a way that the stripes can be uniquely identified from the image. As the figure shows:
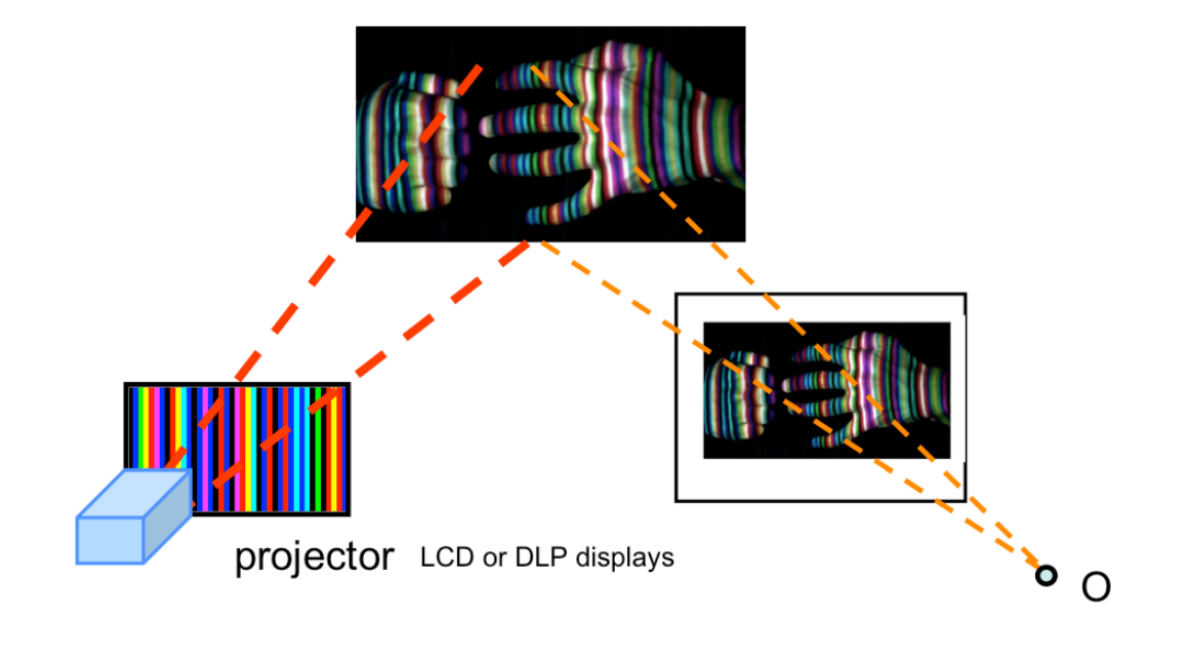
Volumetric stereo
This inverts the problem of using correspondences to find 3D structure: we assume that the 3D point we are trying to estimate is within some contained, known valume and we then project the hypothesized 3D point back into the calibrated cameras and validate whether these projections are consistent across the multiple views. Because these techniques of volumetric stereo assume that the points we want to recover are contained in a limited volume, so these techniques are mostly used for recovering the 3D models of specific objects as opposed to recovering models of a scene, which may be unbounded.A figure explains this: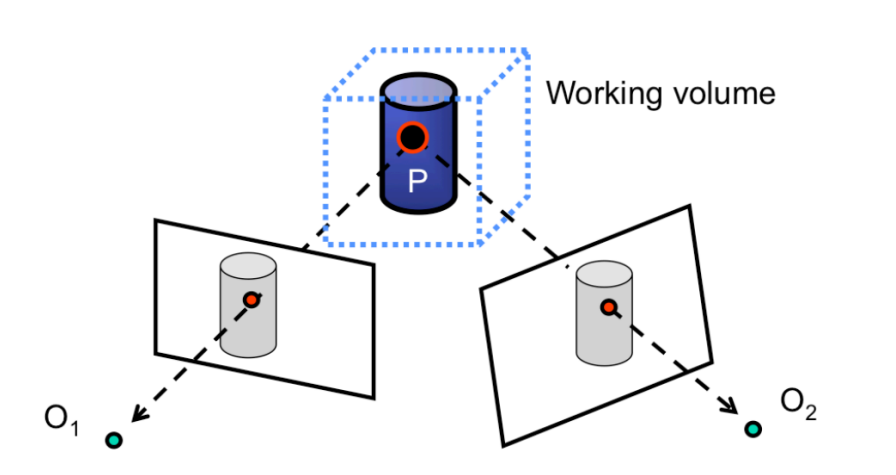
Based on the definition of what it means to "consistent" when we reproject a 3D point in the contained volume back into the multiple image views, we will briefly outline three major techniques:
- space carving
- shadow carving
- voxel coloring
Space carving
This idea derived from that the contours of an object provide a rich source of geometric information about the object. We name the area in the image plane enclosed by the projection of the contours as silhouette. Space carving uses the silhouettes of the object from multiple views to enforce consistency.
Look at the picture: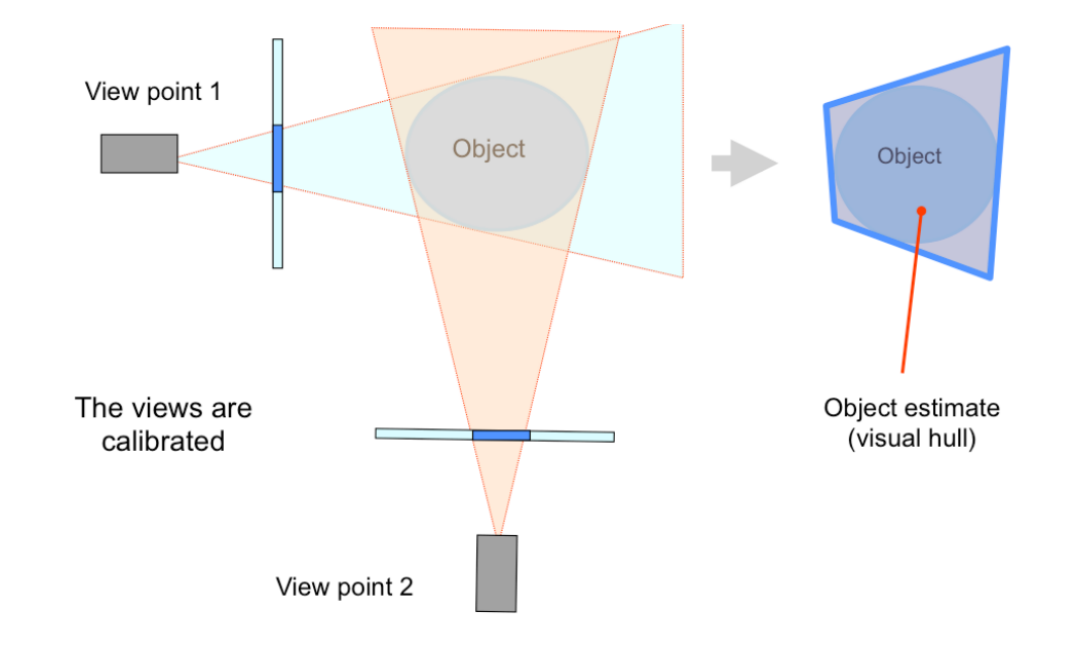
The image center and the object contour in the image plane form an enveloping surface, called visual cone. The object must reside in each of these visual cones and must lie in the intersection of all these visual cones, called visual hull. So we can use the visual hull to estimate the structure of the object.
In real practice, we first need to define a working volume that we know the object is contained within. For example, if our cameras encircle the object, then we can say the working volume is the entire interior of the sapce enclosed by the cameras. We then divide the working volume into samll units, known as voxels (like pixels which is the smallest element of a picture), thus forming what is known as a voxel grid. We take each voxel in the voxel grid and project it into each of the views. If the voxel is not contained by the silhouette in a view, then it is discarded. Consequently, at the end of the space carving algorithm, we are left with the voxels that are contained within the visual hull:
Limitations:
- Time-costing: As we reduce the size of each voxel, the number of voxels required by the grid increases cubically. Therefore, to get a finer reconstruction results in large increases in time.
- Dependency on the number of views, the preciseness of the silhouette, and even the shape of the object we are trying to reconstruct: for example, it is incapable of modeling certain concavities of an object:

Shadow carving
This method is used to circumvent the concavity problem. ONe important cue for determining the 3D shape of an object is the presence of self-shadows. Selfshadows are the shadows that an object projects on itself. For the case of concave objects, an object will often cast self-shadows in the concave region.
The setup: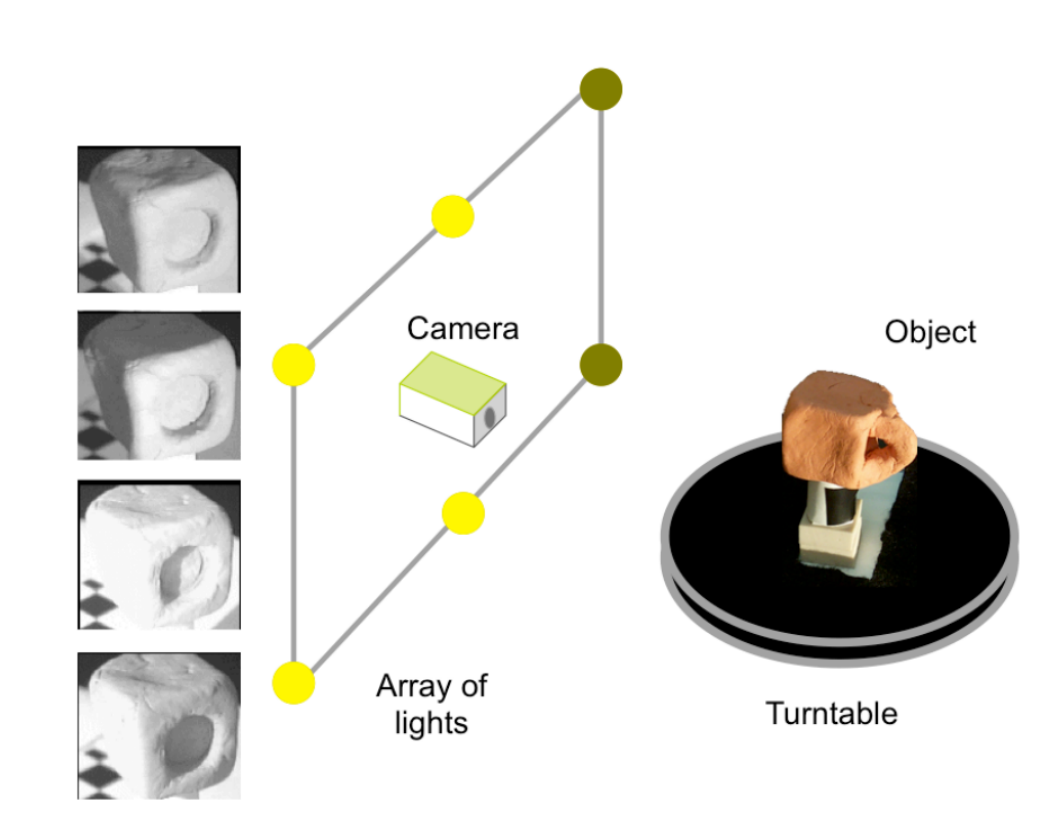
the general setup of shadow carving is very similar to space carving. An object is placed in a turntable that is viewed by a calibrated camera. However, there is an array of lights in known positions around the camera whoes states can be appropriately turned on and off. These lights will be used to make the object cast self-shadows.
First,we use space carving to gain an initial voxel grid. Then in each view, we turn on and off each light in the array surrounding the camera. Each light will produce a different self-shadow on the object. Upon identifying the shadow in the image plane, we can then find the voxels on the surface of the grid that are in the visual cone of shadow. These surface voxels allow us to then make a new visual cone with the image source. We then leverage the useful fact that a voxel that is part of both visual cones cannot be part of the object to eliminate voxels in the concavity. The illustration: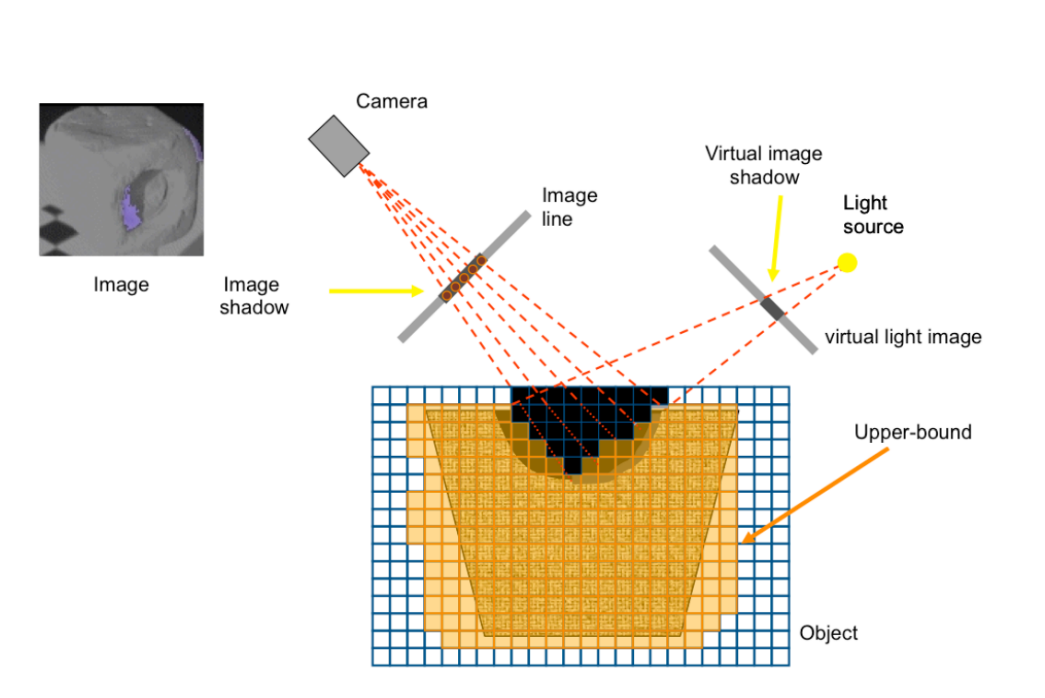
The shadow carving shares similar limitations with space carving: The runtime scales cubically with the resolution of the voxel grid. However, if there are $N $ lights, then shadow carving takes approximately $N + 1$ times longer than space carving, as each voxel needs to be projected into the camera and each of the $N$ lights.
Voxel coloring
This method uses color consistency instead of contour consistency in space carving.
Given images from multiple views of an object that we want to reconstruct. For each voxel, we look at its corresponding projections in each of the images and compare the color of each of these projections. If the colors of these projections sufficiently match, then we mark the voxel as part of the object. One benefit of voxel coloring not present in space carving is that color associated with the projections can be transferred to the voxel, giving a colored reconstruction.
One drawback of vanilla voxel coloring is that it produces a solution that is not necessarily unique. Like this:
In particular, we want to traverse the voxels layer by layer, starting with voxels closer to the cameras and then progress to further away voxels. When using this order, we perform the color consistency check. Then, we check if the voxel is viewable by at least two of the cameras, which constructs our visibility constraint. If the voxel was not viewable by at least two cameras, then it must be occluded and thus not part of the object. Notice that our order of processing the closer voxels allows us to make sure that we keep the voxels that can occlude later processed voxels to enforce this visibility
constraint.